Taggat med: cryptographically secure pseudo-random number generator

Så testar du slumpen

Vid utveckling av kryptografiska produkter eller system är bra slumptal en mycket vital del. Vi har sett många gånger då bristfällig slump leder till katastrofala följder som i fallet med Debians bortoptimerade delar av OpenSSL:

MD_Update(&m,buf,j);
[ .. ]
MD_Update(&m,buf,j); /* purify complains */

Men det finns även andra områden än krypton där bra slump är viktigt. Ta exempelvis TCP ISN som användes av Kevin Mitnick eller nonces och sessionskakor.

Behöver Er organisation hjälp med att testa slumptal? Kontakta Jonas  >

De flesta slumptal som används härstammar från något som heter PRNG (pseudo-random number generator) och betyder att det är pseudo slump som skapas utifrån ett frö (seed). Det finns ett antal olika PRNG algoritmer såsom CryptGenRandom, Blum Blum Shub, Fortuna och Yarrow. Även så brukar man kalla slumptalsalgoritmer som används i krypton för CSPRNG (cryptographically secure pseudo-random number generator)

In the context of a cryptographic system, we have more stringent requirements [than statistical randomness does]. Even if the attacker sees a lot of the random data generated by the PRNG, she should not be able to predict anything about the rest of the output of the PRNG. We call such a PRNG cryptographically strong. […]

Källa: Practical Cryptography

dilbert

Så testar du slumptalsgeneratorn

När du testar slumptal så kan du aldrig vara helt säker på att den alltid kommer att fungera. Det är därför viktigt att genomföra manuella och automatiserade tester löpande. Det är även viktigt att du vet hur dina slumptal kommer att skapas: för är det så att du tar in frövärden/entropi från tangentbord och mus och din kod kommer att köras på en server utan tangentbord och mus.

Ett av de mest kända testbatterierna kallas för Diehard och togs fram runt 1995 av George Marsaglia och senare skapades Dieharder av andra upphovsmän. Även så har NIST ett stort antal resurser såsom dokument och mjukvaror för att testa slumptal, dock så har NIST godkänt slumptalsgeneratorn Dual_EC_DRBG som befaras innehålla en bakdörr (se även extended random). Att köra dessa tester är dock tidsödande men helt klart ett måste.

Om vi skapar en graf så ser vi snabbt att den övre av följande bilder är aningens utstickande (se även view_rng av Joachim Strömbergson):

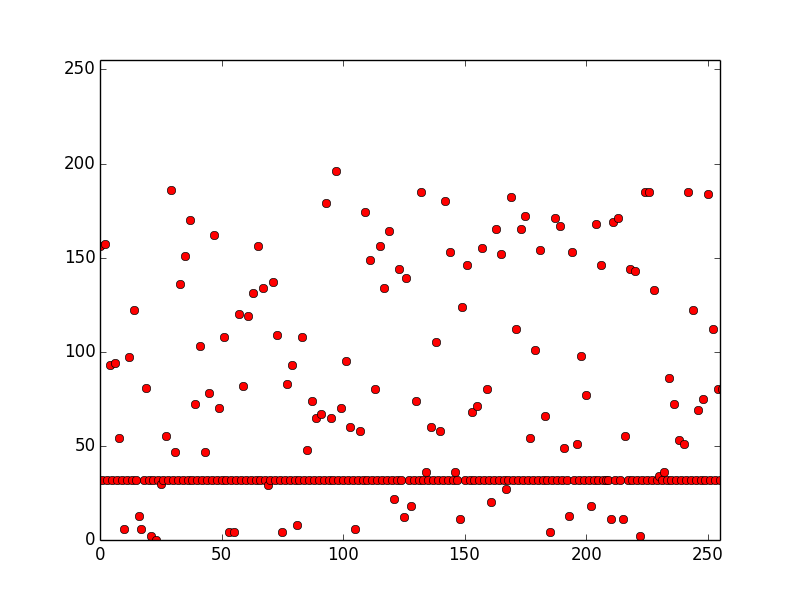
ej slump
Slumpgenerator 1
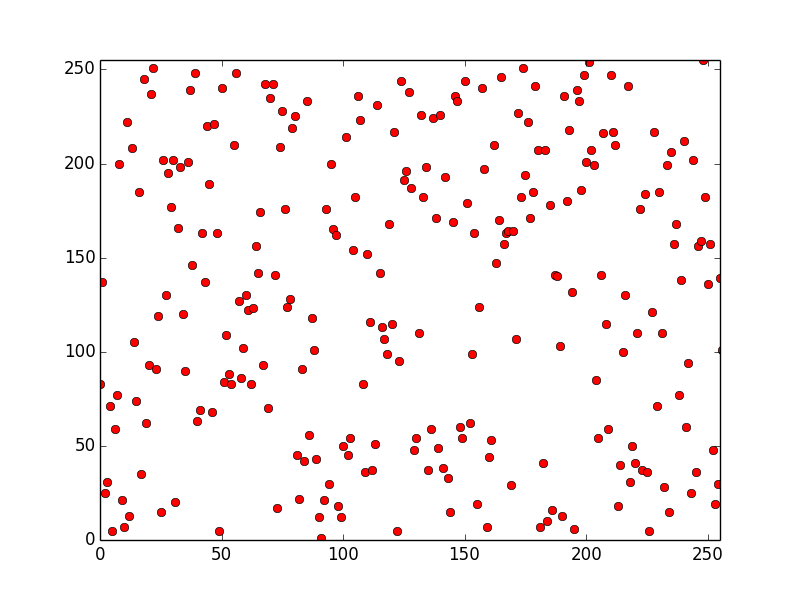
slumptal
Slumpgenerator 2

 

entitleOch använder vi sedan verktyget Ent så ser vi att det är uppenbart vilken slumptalsgenerator som troligtvis genererar dålig slump:

Slumpgenerator 1

Entropy = 4.848706 bits per byte.

Optimum compression would reduce the size of this 98794 byte file by 39 percent.

Chi square distribution for 98794 samples is 6163135.43, and randomly would exceed this value less than 0.01 percent of the times.

Arithmetic mean value of data bytes is 66.3816 (127.5 = random).
Monte Carlo value for Pi is 3.998785302 (error 27.29 percent).
Serial correlation coefficient is -0.419748 (totally uncorrelated = 0.0).

Slumpgenerator 2

Entropy = 7.998370 bits per byte.

Optimum compression would reduce the size of this 100000 byte file by 0 percent.

Chi square distribution for 100000 samples is 225.33, and randomly
would exceed this value 90.97 percent of the times.

Arithmetic mean value of data bytes is 127.6192 (127.5 = random).
Monte Carlo value for Pi is 3.148925957 (error 0.23 percent).
Serial correlation coefficient is 0.000984 (totally uncorrelated = 0.0).

De tester som Ent genomför är bra och kan mycket väl fungera som en grundplattform för vidare tester med exempelvis Dieharder.

Vidare läsning: