NSA varnar för ny Windows-sårbarhet

TL;DR Windows CryptoAPI Spoofing-sårbarhet
Uppdatering: Nu finns det en PoC ute, se nedan bild (källa)
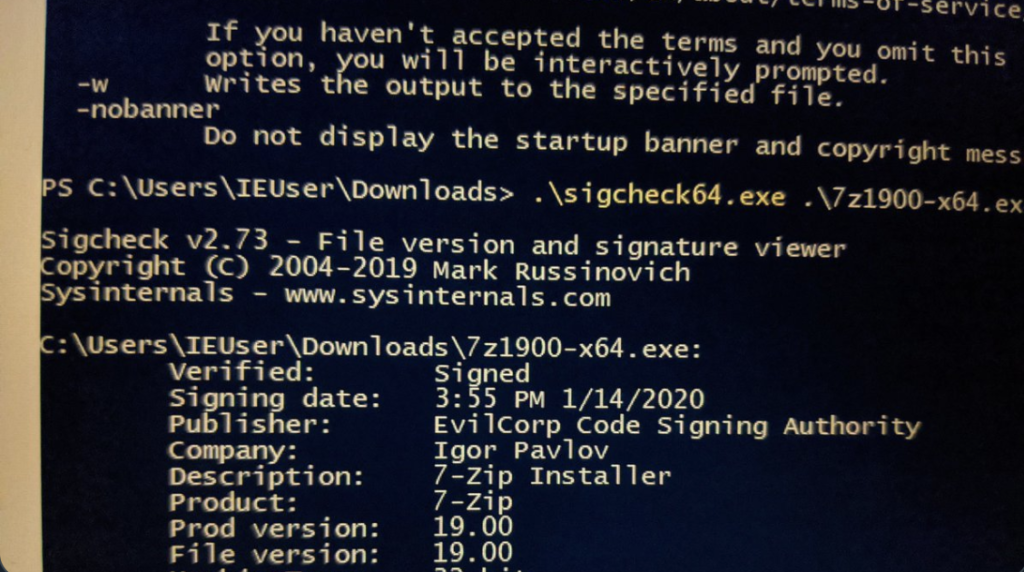
Uppdatering 2: Attacken fungerar även mot Chrome.
NSA gick precis ut och varnade för en ny krypto-relaterad sårbarhet som drabbar samtliga installationer av Windows 10 samt Windows Server 2016/2019. Även påverkade är tredjepartsprogram som använder vissa kryptofunktioner i Windows.
Även skriver NSA att angripare med en god förmåga kommer snabbt att förstå hur dessa sårbarheter kan utnyttjas samt kommer att försöka utnyttja dessa nya sårbarheter.
Exempel där denna bristfälliga signaturvalidering förekommer är:
- HTTPS-anslutningar
- Signerade filer och signerad E-post
- Signerade binärer som startas som användare
Och rekommendationen som åtgärd är att snabbt som ögat installera månadens patchar från Microsoft som släpptes idag. Denna sårbarhet har fått CVE enligt: CVE-2020-0601.
För att upptäcka intrångsförsök eller utnyttjande av bristerna som åtgärdas så kan verktyget certutil eller openssl användas rekommenderar NSA, specifikt på följande sätt:
certutil –asn <certificate_filename>
openssl asn1parse –inform DER –in <certificate_filename> –i –dump
Eller
openssl x509 –inform DER –in <certificate_filename> –text
Håll då koll på avvikande elliptiska kurvor skriver NSA:
Review the results for elliptic curve objects with suspicious properties. Certificates with named elliptic curves, manifested by explicit curve OID values, can be ruled benign. For example, the curve OID value for standard curve nistP384 is 1.3.132.0.34. Certificates with explicitly-defined parameters (e.g., prime, a, b, base, order, and cofactor) which fully-match those of a standard curve can similarly be ruled benign.
Certificates containing explicitly-defined elliptic curve parameters which only partially match a standard curve are suspicious, especially if they include the public key for a trusted certificate, and may represent bona fide exploitation attempts.
Kom ihåg att du även kan läsa ut certifikat från PCAP och nätverkstrafik och sedan granska dem enligt ovan.
Mycket bra att NSA har rapporterat denna brist/brister till Microsoft så en patch kunde släppas. Inga aktiva försöka att utnyttja denna sårbarhet har identifierats rapporterar även Microsoft och NSA.
Varningen i sin helhet kan du läsa här (PDF)



 Google har nu lanserat ett Chrome-plugin som möjliggör PGP-kryptering direkt i webbläsaren med hjälp av OpenPGP. Pluginet går under namnet End-to-End och medger kryptering hela vägen från webbläsaren till slutdestinationen. Observera att det ännu bara är en alfaversion.
Google har nu lanserat ett Chrome-plugin som möjliggör PGP-kryptering direkt i webbläsaren med hjälp av OpenPGP. Pluginet går under namnet End-to-End och medger kryptering hela vägen från webbläsaren till slutdestinationen. Observera att det ännu bara är en alfaversion.